Background

Until now, my only experience with Machine Learning were some simple linear regression excercies. I wanted to deep dive into ML and work on interesting projects for some time now. Using ML to train agents to play games is a popular field for both researcher and enthusiasts. Therefore, I decided to attempt to use ML to train an agent to play the simplest game I can think of: Tic Tac Toe. This page will describe the design though process, implementation, and outcome of my journey.

Project Overview

The project consists of 2 modules: the game and the agent.

The game is implemented in NodeJS. I developed a small framework using JS promises to hanlde the game logic. It was an overkill for this project. Doing it in python would have simplified the design and improved the training performance as well. However, I wanted to keep the board game logic decoupled from the AI Agent's logic. I hope to extend the game's logic into a framework I can later use for other turn-based games (like Chess, or even RPGs). The implementation of the game is out side the scope of this project, however, the entire the source code can be found in the code repository.

The game is flexiable enough to handle different player agents (human, ML, random, etc.) in any order. This info along with other parameters are passed to the game during runtime. For example, first player can be a human and seocnd player can be an ML agent. This helped train the ML agent with different types of player moves.

The agent is a neural network running in python using the pytorch library. A REST API layer is built over the neural network. All interactions between the game and the agent is through HTTP/S. The agent is registered as a player of the game. When the game requires a decision from the agent, it involes the agent's REST API and recieves a decision in the response.

Below is the logical architecture of the project:

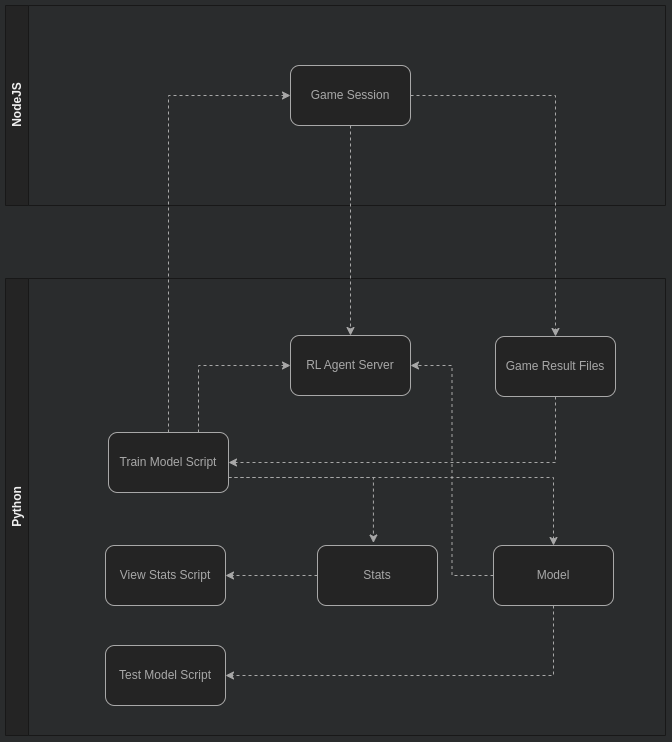
• The RL Agent Server is a python based REST API using the Flask framework. This process can run in the background of the same machine or on a different host machine.
• The train model script invokes the NodeJS game app through CLI. The script batches the number of games per session and repeats the process for the numer of epochs.
• The NodeJS game app creates a session and runs through the sumulation. If one (or two) of the players are ML Agents, the game will invoke the RL Agent Server to get a player decision.
• The NodeJS game app stores the outcome of the game sessions in output files, specified by the train model script.
• The train model script uses the output files to train the neural network. It then invokes the "reload model" endpoint of the RL Agent Server, so the ML Agent is using the latest neural network.

The Environment

In my experience, the hardest part of a Machine Learning project is to figure out how to represent the environment in a way that can be fed into the neural netowrk. When it comes to the actual implementation, libraries like pytorch or tensorflow handles the heavy lifting work (matrix multiplications, backpropagation, optimization, etc.).

In this case, the environment consists of two parts: the board and the active player. I decided to use the same netowrk to train both players. That is why the active player is also part of the input.

There are many ways to represent the environment, each has its own pros and cons. Below are a list of approaches I considered when designing the network.

Bit Encoding

I initially wanted to represent the game environment using bit encoding. The Tic-Tac-Toe board has 9 (3x3) cells. Each cell has 3 states: empty, occupied by player 1 (X), or occupied by player 2 (O). Two bits are requied to represent a single cell:

• 0x00: empty cell
• 0x01: player 1 (X)
• 0x10: player 2 (O)

It would take 20 bits to represent the environment: 18 bits (9 cells x 2 state) + 2 bits for current player. An unsigned integer has 32 bits. Therefore, a single int can be used to represent the entire game environment.

No Encoding (Flat Array)

Next, I tried to use a flat array, without any encoding. In this approach, each cell would take 1 element, and would have the value between 0-2. Where 0 means the cell is free and 1 or 2 means the cell is occupied by player 1 or 2 respectively. An array of size 10 (9 cells + 1 player) is required to represent the game environment. Also, the game uses a flat array to represent the board. Therefore, this was the most straighforward approach.

One Hot Encoding

I finally used the One Hot Encoding. This approach, similar to the previous one, uses a flat array. However, each array element has a value of 0 or 1. It would take 3 elements to represent a sinle cell:

• [1, 0, 0]: empty cell
• [0, 1, 0]: player 1 (X)
• [0, 0, 1]: player 2 (O)

It would take 29 elements to represent the environment: 3x3x3 for the board and another 2 elements for the active player. I used 30 elements for the network to make it even. One Hot Encoding is a good candidate for representing ordinal data, since the data is normalized (0 or 1). Also, the output layer uses the same encoding as well.

The grid below is an interactive demo of the 3 approaches:

Network Architecture

The first step in deciding the network architecute is to figure out what is the learning model (Supervised, Unsupervised, or Reinforced Learning (RL)) for the problem. As the title of the article indicates, Tic Tac Toe is a RL problem. Unlike Supervised / Unsupervised Learning, the network learns the optimal solution through interacting with the environment (the game board).

For this problem, I've decided to use a Deep Q Network (DQN). DQNs have become a popular choice for training neural networks in the video game space. The network uses Off-Policy Learning. In this approach, there are two networks (or policies) with same architecute and weights: Behavior Policy and Target Policy. Behavior Policy is used by the agent to interact with the environment. The Target Policy is the ideal state from which the agent learns from. This process is explained further in the Network Training section.

The network uses 4 layers: input, output and 3 hidden layers.

• The input layer has 30 neurons.
• The first and last hidden layer has 120 neurons.
• The middle hidden layer has 840 neurons.
• The output layer has 9 neurons.
• All layers are fully connected.
• All layers use LeakyReLU as the activation function and dropout is applied to the output.

The input layer takes One Hot Encoded vector of the game board and current player. The neural network returns a One Hot Encoded vector that specifies the next move for the current player.

class Model(nn.Module):
def __init__(self, input_nodes, hidden_layer1_nodes, output_nodes, random=Random()):
    super(Model, self).__init__()
    self.output_nodes = output_nodes
    # fully connected network
    self.fc1 = nn.Linear(input_nodes, hidden_layer1_nodes)
    self.fc2 = nn.Linear(hidden_layer1_nodes, hidden_layer1_nodes*7)
    self.fc3 = nn.Linear(hidden_layer1_nodes*7, hidden_layer1_nodes)
    self.out = nn.Linear(hidden_layer1_nodes, output_nodes)
    self.dropout1 = nn.Dropout(0.1)
    self.leakyReLU = nn.LeakyReLU(0.1)
    self.random = random

def forward(self, x):
    # Apply rectified linear unit (ReLU) activation
    x = self.leakyReLU(self.fc1(x))
    x = self.dropout1(x)
    x = self.leakyReLU(self.fc2(x))
    x = self.dropout1(x)
    x = self.leakyReLU(self.fc3(x))
    x = self.dropout1(x)
    x = self.out(x)
    return x

Network Training

Training Process

The Player Agent takes the current state of the game (board & player) and feeds it to the network. The agent makes a move based on the output of the network. The game evauates the move and moves on to the next player until one player wins the game or there are no valid moves left (game is draw). Once the game session is over, the game stores the results (player actions, winner, draw, etc.) in a session file. The training script, which initiates a batch of sessions, reads the player actions (called "experiences") and stores them in a buffer called the Experience Buffer. Each experience in the buffer has the format:

[State, Action, Reward, Next State]

• State is the One Hot Encoded vector of the current board and player as described in the previous section.
• Action is the player move that was calculated by the network.
• Reward is a numerical value that quantifies effectiveness of the Action on the given State.
• If player is the winner and the the move is the last move then reward is 1.
• If player is loser and the move lost the game then reward is -2.
• If move is an illegal move then reward is -5.
• Default reward is -0.1.
• Next State is the next State of the same player.

For each memory, the Q Value is calculated by the following logic:

if next_state is None:
    q_value = reward
else:
    q_value = reward + discount_rate * max(target_dqn(next_state))

In other words, if the move is the final move, then the Q Value is set to the reward (or penality). However, if there are future moves, then the Q Value is the current reward plus the best next move scaled by a discount rate. The discount rate is a number between zero and one, that determines how much the next state affects the current state. Decreasing the rate will cause the network to ignore long term strategies.

One the Q Value is calculated, the Target Policy's output is updated for the given player move (label). The rest of the flow follows standard ML logic: The loss is calculated between the Behavior Policy's output (y) and the updated Target Policy's output (yhat). Finally, the Behavior Policy's weights are updated through optimization and backpropagation.

def make_qlearning_train_step(policy_dqn, target_dqn, loss_fn, optimizer, discount_rate):
    output_space = set(range(9))

    def train_step(feature, label, reward, next_input):

        # Sets model to TRAIN mode
        target_dqn.eval()
        policy_dqn.train()

        x, options = feature

        # Calculate Q Value
        if next_input is None:
            q_value = torch.tensor(reward)
        else:
            with torch.no_grad():
                # next state's reward is subtracted from current state instead of added
                # because next state is the other player's turn. Therefore, if the other
                # player made a successful move, then that is bad for the current player
                next_x, next_options = next_input
                q_value = reward + (discount_rate * target_dqn(next_x).max())

        # Makes predictions
        y = policy_dqn(x)
        yhat = target_dqn(x)

        # Update target_dqn output with q_value
        yhat = yhat.clone()
        yhat[label] = q_value.item()
        # For all invalid options, set reward to -5
        for i in (output_space - set(options)):
            yhat[i] = invalid_move_score

        # Computes loss
        loss = loss_fn(y, yhat)

        # Computes gradients
        loss.backward()

        # Updates parameters and zeroes gradients
        optimizer.step()
        optimizer.zero_grad()

        # Returns the loss
        return loss.item()

    # Returns the function that will be called inside the train loop
    return train_step

Hyperparameters

Hyperparameter is a parameter that affects the learning process, such as learning rate, optimizer, etc. Selecting the correct hyperparameters is more trail and error than exact science.

learn_rate = 0.00005
discount_rate = 0.9

seed = 0
random = Random(seed)
model_args = {"random": random}
policy_dqn = t3.get_model(filename=model_filename, input_args=model_args)
target_dqn = t3.get_model(filename=None, input_args=model_args)

loss_fn = nn.HuberLoss(delta=1.0) 
optimizer = optim.Adam(policy_dqn.parameters(), lr=learn_rate)
train_step = make_qlearning_train_step(policy_dqn, target_dqn, loss_fn, optimizer, discount_rate)

Training Results

Machine Learning projects usually measure training performance by observing the loss over time. In this case, all player moves are fed into the network inorder to train it. Therefore, observing the loss is useless, because a Non-AI Player (Ex: Random Player) does not use the network to make a decision. Instead, I have used the win ration (# wins / total # of games) to measure the training accuracy.

The game supports the following players:

• Human Player: a human needs to enter the next for the player.
• Random Player: the agent makes a random valid move for the player.
• AI Player: the agent feeds the current state into the DQN and uses the output layer to make the next move for the player.
• Heuristic Player: the agent makes valid random choices until it is either about to win or lose in the next turn. In which case, it will either make the winning move or prevent the other player from winning.

The next section contains training results against different types of players. The X-axis is the number of epochs and the Y-axis is the number of wins. All trainings were conducted with 400 epochs and 100 game sessions per epoch. I've set it so neither player could be disqualified (DQ'ed).

AI Player vs Random Player

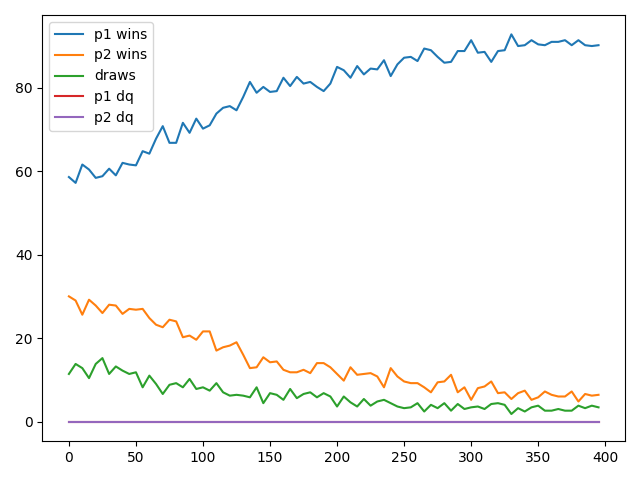
This case demonstrates how biased the game really is. The first player has significant advantage over the second player, simplify by going first.

Random Player vs AI Player

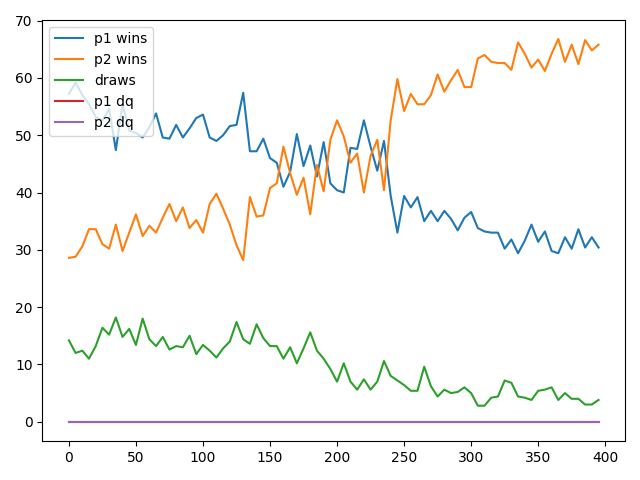
In this case, the second player is the AI Player. The AI Player began with a win rate of 30%, while the Random Player had a win rate of 60%. Around 200 epochs (20,000 game sessions), the AI Player began to out perform the Random Player. By 400 epochs, the AI Player is winning about 70% of the time.

Heuristic Player vs AI Player

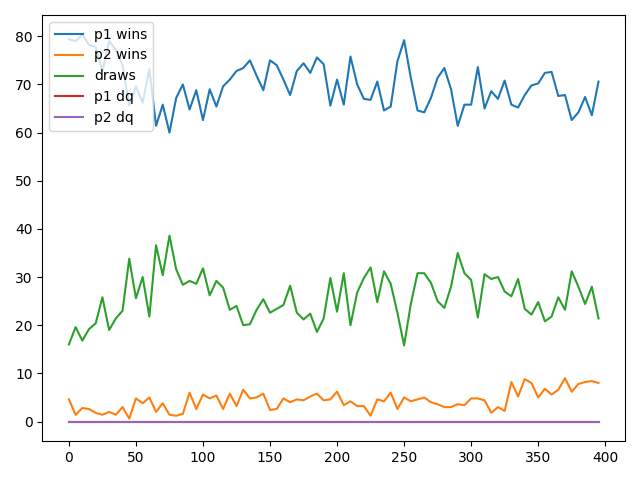
In this case, the AI player was second player, and got oblliterated by the Heuristic Player. The AI player started with around 20% win rate. After 400 epochs, the win rate remained around 20%. So very little learning ocurred.

AI Player vs Heuristic Player

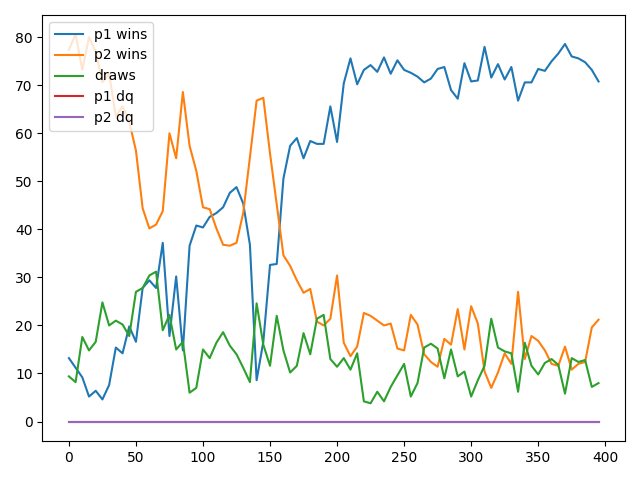
I wasn't very optimistic after the last round, but was surprised to see the results. The AI player started with a win rate of little over 10%. Around 150 to 200 epochs, it began to out perform the Heuristic Player. By 400 epochs, it's winning rate rose to about 70%.

Conclusion

Training an agent to play Tic Tac Toe was alot harder than I thought. Evan after fixing the initial silly python bugs in the code, the network simply was not learning from the game sessions. I've tried alot of things to fine-tune the hyperparameters (increasing layers & neuron size, various activation & loss functions, normalization, dropout, etc.) most of which yeilded little improvement. Ultimately, I beleive decreasing the learning rate and adding "guard rails" to penalize invalid moves made a difference.

Future Works

Following are some areas for possible improvements:

• Use seperate set of networks for each player. Instead of having a single pair of DQNs (Behavior + Target policies), it maybe more optimal to have 1 pair of DQNs for player 1 and another for player 2.
• Experiment with different types of networks. So far, all training was conducted on Fully Connected Neural Networks. Perhaps Convolutional Neural Networks (CNNs) might yeild better results.
• Use cyclic learning rate when training the network.

Final Thoughts

While I was hoping for a 90% success rate, I am satisfied with 70%. The agent showed significant learning improvement and out performed it's opponent in 3 out of 4 cases. I think I've played more games of Tic Tac Toe in last 3 months than I did in my childhood, so I am ready to move on. If I decide to come back to this project in the future, and make any significant progress, I will update this section.

Reference

View the entire code in the Github Repository